物理教室

問題６　[e]の解答

「小物体が曲面から離れることなく」と問題文に書いてあります。
小物体が曲面から離れない条件は
小物体に働く垂直抗力　≧　０
です。
小物体の運動が円運動になるのはQ点からですので
「Q点からR点までの間、小物体に働く垂直抗力が０以上」であれば曲面から離れることなくR点にたどり着くことが出来ます。

Q点とR点の間のある位置に小物体がある時を考えてみます。
その時、
小物体とOとRがなす角度を上図のようにφとし、
小物体に働く垂直抗力をN_φ、
小物体の速度をv_φとします。
小物体に働く力は、重力と垂直抗力の二つですから
小物体に働く垂直抗力N_φは
[d]で求めた垂直抗力において
小物体の速度をv_Qからv_φ、
　　　　　角度をθからφにしてあげたものになります。
したがって

となります。
Q点からR点の間でφは
０≦φ≦θ
の範囲を動きます。
「Q点からR点までの間、小物体に働く垂直抗力が０以上」になるためには
垂直抗力N_φについて、 Q点からR点までの間で
最小のN_φ≧０
ならQ点からR点までの間、曲面から離れることはありません。
では、 ０≦φ≦θにおける 最小のN_φについて考えてみましょう。
φが変化すると共に変化するのはcosφとv_φです。

　　〜cosφについて〜
０≦φ≦θにおいてcosθ≦cosφ≦１より
Q点でcosφは最小になる。

〜v_φ² について〜
小物体がQ点からR点まで動いている間、小物体に外力は働かないので力学的エネルギー保存則が成り立ちます。
位置エネルギーの基準をQ点として
Q点と小物体、O、Rのなす角度がφの点とで力学的エネルギー保存則を立ててあげると

０≦φ≦θにおいて、cosφ- cosθ≧０よりmgr(cosφ- cosθ)≧０
したがってQ点からR点の間では、Q点での小物体の速さが最大になります。
（エネルギー保存則において「Q点の運動エネルギー」から「角度がφの点の運動エネルギー」を引いた値が正になるから。）
v_R²≦v_φ²≦v_Q²より
−v_Q²≦−v_φ²

以上よりQ点での垂直抗力が最小であることがわかります。
したがってQ点からR点までの間、小物体が曲面から離れない条件は N_Q≧０

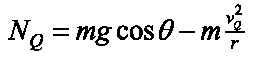
より

r > 0であるから
grcosθ≧v_Q²
また、Q点とR点の力学的エネルギー保存則より

であるから
v_Q²=v_R²+2gr(1-cosθ)
この式を曲面から離れない条件に代入してあげると
grcosθ≧v_R²+2gr(1-cosθ)
3grcosθ-2≧v_R²

求めたい答えは

問題６　[f]の解答 へ

ページの先頭へはこちら

---